Getting to the bottom of "the square"

If you ask me about the research I'm doing on compositional algorithms I'll probably tell you about "the square". In its most abstract form, the square looks like this:

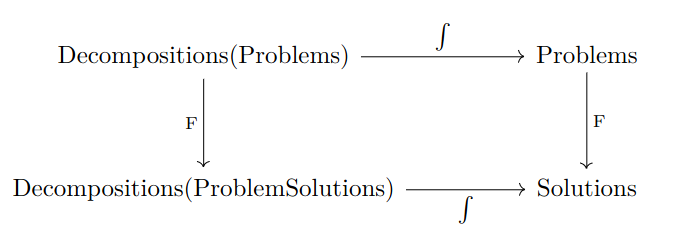
If you start with a decomposition of a problem, there are two ways to go:

1. Turn the decomposition of your problem into a single problem and then find the solution
2. Turn your decomposition of problems into a decomposition of solutions and then glue those solutions together.

Going right then down is number 1 and going down then right is number 2. Method 2 is the "compositional solution" which is often preferable to 1 for efficiency and reliability reasons. On the contrary, method 2 is the "naive solution" which does not use any information about the decomposition to compute the answer. If the square commutes (at least up to iso), then we know that the compositional solution is correct because it corresponds to the naive solution.

I am particularly interested in instances of this square when the gluing comes from the Grothendieck construction. In the case when the problem functor $ F: \mathrm{Problems} \to \mathrm{Solutions}$ solves the algebraic path problem (c. f. https://arxiv.org/abs/2005.06682) the horizontal sides of "the square" come from the enriched Grothendieck construction of Liang Ze Wong and Jonathan Beardsley.

In particular, when enriching in the min-plus semiring $ ([0,\infty],\mathsf{min},\mathsf{+})$ "the square" represents a compositional solution to the shortest path problem. I wrote a paper "How to Compose Shortest Paths" which proved a compositionality result about the shortest path problem (without using the square, just with matrix algebra) and implemented an algorithm that had very encouraging results.

There is an instance of the square when $ F$ solves the safety problem as in my last post. I conjecture that this square comes from a $ \mathsf{Bool}^{op}$-enriched Grothendieck construction although I do not yet have proof that the square exists or commutes (indeed I called it a "theorem of the heart").

There should also be an instance of the square when the problem functor solves the safety problem for Petri nets. This problem asks: "starting in a set of markings I, will the set of reachable markings of a Petri net P be contained in a subset of markings F". There should be another related functor where the problem functor computes the category of of processes of the net as in the famous paper "Petri Nets are Monoids". I am highly interested in both these cases because Petri nets can be relatively realistic models of the real-world.

So I want to get to the bottom of all these squares. I want to see which squares give useful algorithms and also prove that these algorithms are correct. I want to understand which of these squares can be understood as instances of a more general family of squares. In an ideal world, I could prove correctness for this general family of squares all at once.

This is a very ambitious project and completely understanding the principles of "the squares" will probably take at least a few years. It is all very intimidating so I will start small with the square that I already have worked out.

The topic of my next blog post will be a square corresponding to a compositional algorithm for the "free category on a graph". The free category on a graph is roughly representative of the sort of problems I am interested in. Indeed, I structured my Ph.D thesis around this idea and specializing to enriched and internal free categories. I will explain this square next time but here is a picture of it:

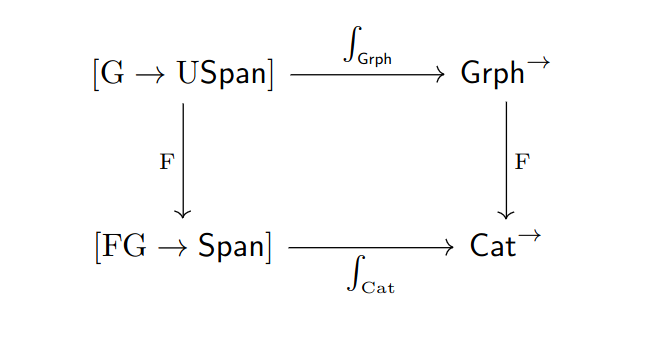
See you next time!