How to Stay Locally Safe in a Global World (Part III: The Global Safety Poset)
by Jade Master
In this post we will propose a compositional solution to the local safety problem in a global context (as defined in Part II) in two steps:
- First by turning the world into a functor $ \hat{W} : FG \to \mathsf{Poset}$
- Then by gluing this functor into a single poset $ \int \hat{W}$ whose inequalities solve the problem of interest.
First we define the functor.
Given a world $ W : G \to \mathsf{Mach}$, there is a functor
$ \hat{W} : FG \to \mathsf{Poset}$
where
- $ FG$ is the free category on the graph $ G$,
- $ \mathsf{Poset}$ is the category whose objects are posets and whose morphisms are monotone functions.
Functors from a free category are uniquely defined by their image on vertices and generating edges.
- For a vertex $ x \in V(G)$, $ \hat{W}(x) = \mathcal{P}(S_x)$,
- for an edge $ e : x \to y$, we define$ \hat{W}(e): \mathcal{P}(S_x) \to \mathcal{P}(S_y)$ by
$ A \mapsto \blacksquare_{W(e)}(A)$ (defined as in Part I)
Now for step two.
Given a functor $ \hat{W} : FG \to \mathsf{Poset}$ defined from a world $ W$, the \textbf{global safety poset} is a poset $ \int \hat{W}$ where
- elements are pairs $ (x \in V(G), A \subseteq S_x)$,
- $ (x, A) \leq (y, B) \iff$
$ \bigwedge_{f: x \to y \in FG} \hat{W} (f) (A) \subseteq B$
I have not fully formed a proof of the following theorem yet, it is still a theorem of the heart (a phrase I borrowed from my graduate analysis textbook meant to mean a theorem without a proof but nevertheless believed to be morally true).
Theorem: Given a world $ W : G \to \mathsf{Mach}$, a vertex $ x \in V(G)$, and subsets $ I,P \subseteq S_x$ then $ I$ is locally safe in a global context if and only if there is an inequality
$ (x,I) \subseteq (x,P)$ in the global safety poset $ \int \hat{W}$.
My half-completed proof of this theorem involves a square of functors
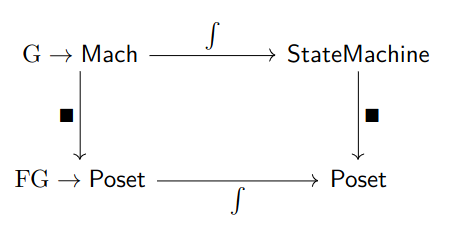
Going from right and then down, the first functor uses a Grothendieck construction to turn a world into a total state machine and then turns that state machine into it's global safety poset. Going down and then right follows the construction detailed in my past two posts. The commutativity of this diagram should verify correctness. I will explain all of this in more detail later. Thanks for tuning in today!