How to Stay Locally Safe in a Global World (Part II: Defining a World And Stating the Problem)
by Jade Master
Suppose we have a directed graph $ G=(V(G),E(G))$ representing our world. The vertices of this graph are the different agents in our world and an edge represents a connection between these agents. The semantics of this graph will be the following:
Definition: Let $ \mathsf{Mach}$ be the directed graph whose objects are sets and where there is an edge $ e : X \to Y$ for every function
$ e : X \times \Sigma \to \mathcal{P}(Y)$
A world is a morphism of directed graphs $ W : G \to \mathsf{Mach}$.
A world has a set $ S_x$ for each vertex $ x$ called the local state over $ \mathbf{x}$ and for each edge $ e :x \to y$ a function $ W(e) : S_x \times \Sigma_e \to \mathcal{P}(S_y)$ representing the state machine connecting the local state over $ x$ to the local state over $ y$. Note that self edges are ordinary state machines from a local state to itself. A drawing of a world is below.
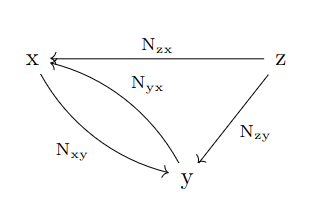
Definition: Given a world $ W: G \to \mathsf{Mach}$, the total machine of $ W$ is the state machine
$ \int W : \sum_{x \in V(G)} S_x \times \sum_{e \in E(G)} \to \mathcal{P}( \sum_{x \in V(G)} S_x )$
given by
$ (s,x),(\tau,d) \mapsto \bigcup_{e: x \to y} F(e) (s, \tau)$
The notation $ \int$ is used based on the belief that this is some version of the Grothendieck construction. Exactly which flavor will be left to future work. The transition function of this state machine comes from unioning the transition functions of all the state machines associated to edges originating in a vertex.
Definition: Given a world $ W : G \to \mathsf{Mach}$, a vertex $ x \in V(G)$, and subsets $ I,P \subset S_x$, we say that $ I$ is locally safe in a global context if
$ \mu (\blacksquare_{\int W} (-) \cup I) \subseteq P$
where $ \blacksquare_{\int W}$ is the next-time operator of the state machine $ \int W$.
The state machine $ \int W$ may be large enough to make computing this least fixed point by brute force impractical. Therefore, we must leverage the compositional structure of $ W$. We will see how to do this in the next post.