What is a Graph Decomposition?

I've been working lately on developing a categorical framework for reasoning about compositional graph algorithms. Before discussing this framework I need to define its main object of study: a graph decomposition. I've made a stab at defining graph decompositions (as structured decompositions) with Ben Bumpis and Zoltan Kocsis. After working some more, I've arrived at new definition of graph decomposition. I'd like to present this definition here. This definition aims to follow Grothendieck's definition of indexed category, but adapted to the case of weighted graphs. Surprisingly, the definition involves no categories.

Definition: For a semiring R, an R-graph is a function $ G: X \times X \to R$

X is the set of vertices, the value G(x,y) gives the weight from vertex x to vertex y.

Example: Let B be the semiring $ \{0,1\}$ with "or" as the sum and "and" as the product. Then a B-graph is a directed graph without multiple edges.

Sometimes R will also have the structure of a category. Traditional weighted graphs are weighted in a poset. In this case there is a unique morphism from x to y if and only if $ x \leq y$. We also want to consider graphs weighted in $ \mathsf{Set}$, the category of sets and functions. This is technically not a semiring, but we can pretend like it is with disjoint union as its addition and cartesian product as its product. There's a long story about this that I will not speak of now.

Example: A $ \mathsf{Set}$-graph is a labelled directed multigraph.

Example of the example: Let $ \mathsf{RMat}$ be the $ \mathsf{Set}$-graph where a vertex is a set X and an edge from X to Y is a function $ f : X \times Y \to R$

$ \mathsf{RMat}$ has large sets of vertices and edges, and I mean this in a technical sense. We also need morphisms between R-graphs.

Definition: A R-graph morphism with source $ G: X \times X \to R$ and target $ H: Y \times Y \to R$ is a function $ f: X \to Y$ along with an R-morphism

$ f_{x,y} : G(x,y) \to H(f(x),f(y)) $

for each pair $ x,y \in X$.

Definition: A For a B-graph $ G : X \times X \to B$, the free $ \mathsf{Set}$-graph on G, is $ G_{\mathsf{Set}} : X \times X \to \mathsf{Set}$ is given by setting $ G_{\mathsf{Set}}(x,y)$ to a chosen 1 element set if $ G(x,y)=1$ and setting it to the empty set otherwise.

We are now finally ready for the definition of an R-graph decomposition.

Definition: An R-graph decomposition is a morphism of $ \mathsf{Set}$-graphs

$ D : G_{\mathsf{Set}} \to \mathsf{RMat}$

for a B-graph G.

G is called the shape of the decomposition. For a vertex x of G, D(x) is called the bag sitting above x and for an edge $ e: x \to y$ the R-matrix $ D(e) : D(x) \to D(y)$ is called the adhesion sitting above e.

Example: Let R be the semiring $ [0,\infty]$ of positive real numbers and infinity (semiring structure left unstated). Suppose G is the B-graph

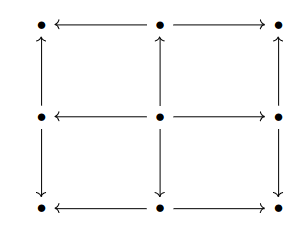
then a $ [0,\infty]$-graph decomposition of shape G is drawn as

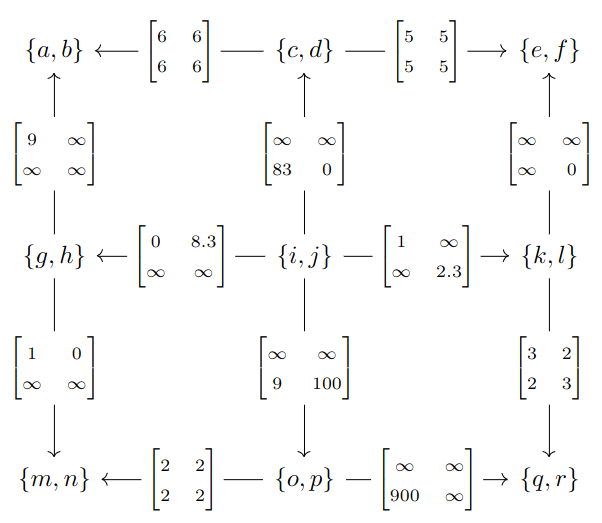
with bags and adhesions drawn sitting over their corresponding vertices and edges of G. Eventually I will explain how a decomposition such as this may be used to find the shortest paths in a graph more efficiently.

I think this definition good because it strikes a nice balance between abstract and concrete. However, I chose this definition because it admits a variant of the Grothendieck construction. Roughly, decompositions of this sort are equivalent to ordinary morphisms of R-graphs. Stay tuned for the details of this in my next post.