The Fibrational Perspective on Graph Decompositions
by Jade Master
In my last post, I proposed a definition of "weighted graph decomposition" modeled after Grothendieck's indexed categories. Indexed categories are most well-known from their use in the eponymous Grothendieck Construction. Essentially, the Grothendieck construction turns a functor $ F: C^{op} \to \mathsf{Cat}$ into a functor $ G : \int G \to C$ such that F is like the inverse mapping of G. To learn more about the Grothendieck construction please read my series of blog posts starting here: Let’s Grothendieck Everything in Sight (Week 1). It turns out that there is a version of the Grothendieck construction specialized to graph decompositions that I will explain now.
Definition: Let R be a semiring with additive unit $ 0_R$ and multiplicative unit $ 1_R$. Let $ G: X \times X \to B$ be a B-graph where B is the boolean semiring. The free R-graph $ G_R: X \times X \to R$ on G is the R-graph given by $ G_R(x,y)=1_R$ if $ G(x,y)=1$ and by $ G_R(x,y)=0_R$ otherwise.
Next we define a different but equivalent perspective on R-graph decompositions. Please recall from the previous post the definition of R-graph morphism.
Definition: A fibrational R-graph decomposition is an R-graph morphism
$ f : H \to G_R$
Example: Suppose R is $ [0,\infty]$ with the min-plus semiring structure where $ 0_R=\infty$ and $ 1_R=0$. Recall that for each pair x, y in a R-graph G, we must have a weight G(x,y) in R. In the picture below, vertices which do not have an edge connecting them are assumed to have weights of $ 0_R=\infty$.
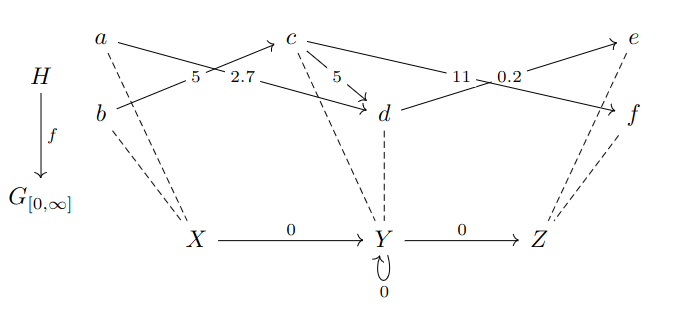
Just like a dependent graph decomposition, a fibrational graph decomposition has a shape graph, bags, and adhesions. The shape graph of this fibrational decomposition is a B-graph G. For a vertex x of G, the bag sitting above x is the set $ f^{-1}(x)$. For a pair of vertices in G with weight $ G(x,y)=0$, the adhesion above x and y is the subgraph of H consisting of the edges which start in the bag sitting above x and end in the bag sitting above y.
A fibrational graph decomposition has a feature which a dependent graph decomposition does not: the total graph. The total graph may be immediately obtained from a fibrational R-graph decomposition.
Definition: The total graph of a fibrational R-graph decomposition $ f: H \to G_R$ is the R-graph H.
On the other hand, to get a total graph from a dependent R-graph decomposition, we have to glue its pieces together.
Definition: For a dependent R-graph decomposition $ D: G_{\mathsf{Set}} \to \mathsf{RMat}$, its total graph is the R-graph $ \int D$ whose vertices are elements of the set
$ \{ (x,a) \, | \, x \in Vert(G) \text{ and } a \in D(x)\}$
and for vertices $ (x,a)$ and $ (y,b)$, their weight is given by
$ \int G( (x,a),(y,b)) = D(x,y)(a,b)$
Furthermore, $ \int D$ has a natural R-graph morphism $ \int D \to G_R$ which forgets the second component of each vertex. So the total graph we defined starting from a dependent R-graph decomposition is actually a fibrational R-graph decomposition.
Example:
This dependent $ [0,\infty]$-graph decomposition
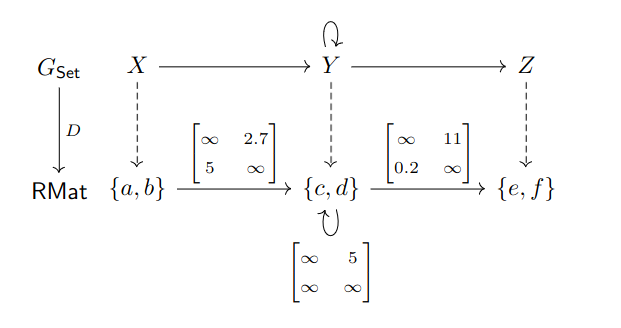
corresponds to the fibrational R-graph decomposition
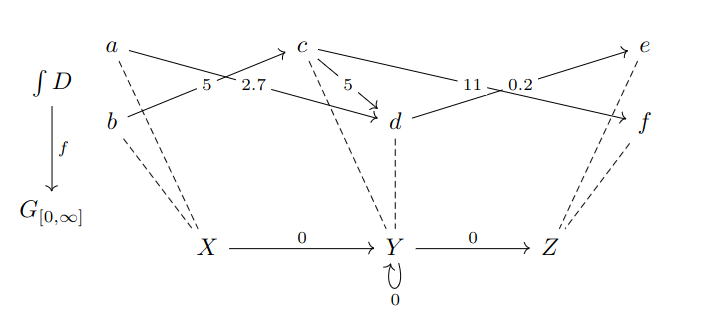
shown in the previous example. The total graph $ \int D$ of the previous definition is the top row of the above picture. On the other hand, if we start with a fibrational R-graph decomposition we may obtain a dependent R-graph decomposition by taking preimages.
Definition: Let $ f: H \to G_R$ be a fibrational R-graph decomposition. Then the dependent R-graph decomposition $ f^{-1} : G_{\mathsf{Set}} \to \mathsf{RMat}$ is given by $ f^{-1}(x)$ for a vertex x of G. For an edge from x to y in G, $ f^{-1}$ maps this edge to the full subgraph of H consisting of the edges with source in $ f^{-1}(x)$ and target in $ f^{-1}(y)$.
From the example, you may be able to see how the operations $ \int$ and $ ^{-1}$ undo each other. Indeed, these two maps form an equivalence between suitable structures of dependent and fibrational graph decompositions. Stay tuned for my next post where I will hammer out the details of this equivalence.