Euler's Method as a Free Category
by Jade Master
In this blog post I will show how the numerical solutions to a differential equation using Euler's method can be represented as a free category on a graph. Given a vector field
$ v: \mathbb{R}^n \to \mathbb{R}^n$
and a step size $ h>0$, you can form a graph whose vertices are elements of $ \mathbb{R}^n$ and whose edges advance Euler's method by one time step. The free category on this graph then contains all runs of Euler's method on v for all possible lengths of time.
what is Euler's method?
Let $ v: \mathbb{R}^n \to \mathbb{R}^n$ be a vector field i.e. a smooth function. Euler's method computes an approximate solution to the differential equation
$ \frac{d\mathbf{x}}{dt} = v(\mathbf{x})$
where $ \mathbf{x}$ is a vector in $ \mathbb{R}^n$. The core of Euler's method is the equation
$ \mathbf{x}(t+h) = \mathbf{x}(t) + h v(\mathbf{x}(t))$
where h is a positive real number. Given an initial condition $ \mathbf{x}(0) = \mathbf{x_0}$ an approximate solution can be computed by repeatedly applying the above equation.
the categories in question
Let $ \mathsf{Span(V,V)}$ be the category where
- objects are spans $ V \leftarrow A \to V$ and,
- a morphism from $ V\leftarrow A \to V$ to $ V \leftarrow B \to V$ is a function $ f: A \to B$ commuting with the functions in each span
Note that $ \mathsf{Span(V,V)}$ is a category where objects are graphs with vertex set V.
Let $ \mathsf{Cat(V)}$ be the category where
- objects are categories whose objects are elements of V and,
- morphisms are functors between such categories.
the free category construction
There is a forgetful functor
$ U : \mathsf{Cat(V)} \to \mathsf{Span(V,V)}$
which sends a category to it's underlying graph and a functor to its underlying morphism of graphs. Then U has a left adjoint
$ F : \mathsf{Span(V,V)} \to \mathsf{Cat(V)}$
generating for each graph a category whose morphisms contain all possible composites of edges. The idea is that given a graph
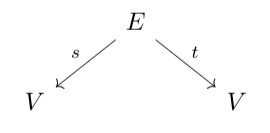
we can put another copy next to it and take the pullback
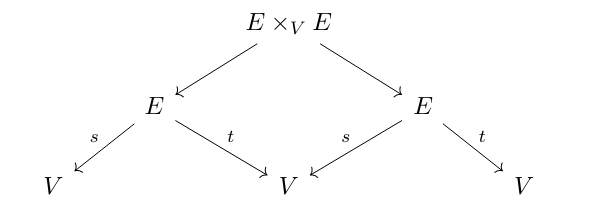
Explicitly, this pullback is the set
$ E \times_V E = \{ (a,b) \in E \times E \, | \, t(a) = s(b) \}$
i.e. the set of composable pairs of edges. This pullback can be iterated. In general for a natural number n, the n-th pullback is the set
$ E^n = \{ (a_1,a_2, \ldots, a_n) \, | \, t(a_1)=s(a_2), t(a_2)= s(a_3) \ldots t(a_{n-1}) = s(a_n) \}$
i.e. the n-tuples of composable edges. To get all composable edges of any length we need to combine all these sets. Indeed, the free category has morphisms given by the infinite coproduct
$ \sum_{n=0}^{\infty} E^n$
where the 0-th pullback is defined to be the vertex set V. This free category has composition given by concatenation of tuples.
putting the ingredients together and baking the cake
The key is to consider the span
$ A=\mathbb{R}^n \xleftarrow{1} \mathbb{R}^n \xrightarrow{1 + h v} \mathbb{R}^n$
where $ 1$ is the identity function and $ 1 + hv (\mathbf{x}) = \mathbf{x} + h v(\mathbf{x})$. The k-th pullback of this span with itself is the set
$ \{ (x_1,x_2,\ldots, x_k) \in \mathbb{R}^{n \times k}\, | \, x_2 = x_1 + h v(x_1),\ldots, x_{k} = x_{k-1} + hv(x_{k-1}) \}$
i.e. k time steps of Euler's method applied to $ v(x)$. The free category on this span has morphisms given by the coproduct of all these sets so we have that:
F(A) is a category where
- objects are elements $ \mathbf{x} \in \mathbb{R}^n$ and,
- a morphism from $ \mathbf{x}$ to $ \mathbf{y}$ is tuple $ (x=x_1, \ldots, y=x_k)$ which is an approximate solution to $ \frac{d\mathbf{x}}{dt} = v(\mathbf{x})$ using Euler's method with step size h.
Thank you for reading!