Dynamical Systems with Category Theory? Yes!

Sadly, this post is not about the Grothendieck construction. However, it will lay the groundwork for a Grothendieck construction in the future. This post is about understanding dynamical systems from the point of view of category theory.

Topologists love convenient categories. But you may have not know that dynamical systemists (?) often desire convenience as well. In Convienent Categories of Smooth Spaces Baez and Hoffnung tweak the definition of smooth manifold to make the category $ \mathsf{Diff}$ of diffeological spaces. The key difference between manifolds and diffeological spaces is that manifolds have charts which go from your manifold to an open subset of $ \mathbb{R}^n$ and diffeological spaces have plots which go in the opposite direction; from an open subset of $ \mathbb{R}^n$ to your diffeological space. This category has lots of conveniences but the one that I'm most interested in is the existence of an internal "hom". This means the following fact:

For two diffeological spaces $ M$ and $ M'$, the set of smooth maps $ \mathsf{Diff} ( M , M')$ is naturally equipped with the structure of a diffeological space.

I don't plan to go into the details of diffeological spaces but for the purposes of this post you can think of them as smooth manifolds which can possibly have infinite dimension. Indeed there is a nice fully faithful embedding of the category of smooth manifolds into $ \mathsf{Diff}$.

Okay now let's get moving with dynamical systems (sorry).

A dynamical system is roughly the solution to a system of ordinary differential equations. A slick definition is the following:

Definition: A dynamical system or flow on a manifold $ M$ is a group homomorphism

$ \phi : (\mathbb{R}, + ) \to \mathrm{Aut}(M)$

where $ \mathrm{Aut}(M)$ is the group of diffeomorphisms from $ M$ to itself.  The idea is that your system of ordinary differential equations is given by some vector field on $ M$. For a given time $ t$, $ \phi(t)$ calculates a new position, on all points of your manifold at once, in the direction of your vector field after $ t$ elapses. You want the flow to have several nice properties.

• For every $ t$, $ \phi(t)$ should be a diffeomorphism
• Advancing for time $ t$ and then advancing for time $ t'$ should be the same as advancing for time $ t+t'$. This means,

$ \phi(t +t') = \phi(t') \circ \phi(t)$

• Advancing for no amount of time should be the identity function on $ M$. This means

$ \phi(0) = 1_M$

These conditions can be succinctly described by the definition above!

If you're a sneaky category theorist you may have heard of the following fact:

Proposition: Let $ M$ be an object in a category $ C$ and let $ \mathrm{Aut} (M)$ be the group of isomorphisms of $ M$. Then a group homomorphism $ \phi : G \to \mathrm{Aut} (M)$ specifies a unique functor

$ \phi : G \to C$

where $ G$ is regarded as one object category with the group elements as morphisms and $ \phi$ sends the unique object of $ G$ to $ M$.

Proving this is a fun exercise if you haven't seen it before. The idea is that the homomorphism property means that the assignment given by $ \phi$ preserves composition. Because homomorphisms preserve identities and composition the morphisms in the image of $ \phi$ must all be isomorphisms.

So far we have that a functor $ \phi : \mathbb{R} \to \mathsf{Diff}$ characterizes the data of a dynamical system...except for the requirement that $ \phi$ is smooth. To capture this we can use enrichment.

Proposition: A dynamical system is a $ \mathsf{Diff}$-enriched functor

$ \phi : \mathbb{R} \to \mathsf{Diff}$

Proof: Like most proofs in category theory, this proof relies on unpacking the definitions and seeing that the claim is true. First we need to understand how $ \mathbb{R}$ and $ \mathsf{Diff}$ are $ \mathsf{Diff}$-enriched categories. There is only one hom-set in $ \mathbb{R}$ and it's given by the real numbers. This is one of nicest examples of diffeological spaces. Because the set of smooth maps between diffeological spaces is again diffeological space, $ \mathsf{Diff}$ is enriched in itself.

A $ \mathsf{Diff}$-enriched functor $ F : C \to  D$ consists of a smooth map $ \mathrm{Hom} (x,y) \to \mathrm{Hom} (Fx, Fy)$ for every pair of objects $ x$ and $ y$ in $ C$. Because there is only one pair of objects in $ \mathbb{R}$ we get just one smooth map. The axiom requiring that $ \phi$ respects composition and the axiom requiring that $ \phi$ preserves identities (found here) are equivalent to $ \phi$ being a group homomorphism.

Dynamical system theorists are interested in comparing dynamical systems. For this they invented the idea of topological conjugacy.

Definition: Let $ \phi$ and $ \phi'$ be dynamical systems on manifolds $ M$ and $ M'$ respectively. Then a topological conjugacy from $ \phi$ to $ \phi'$ is continuous map

$ f : M \to M'$

such that the following diagram commutes

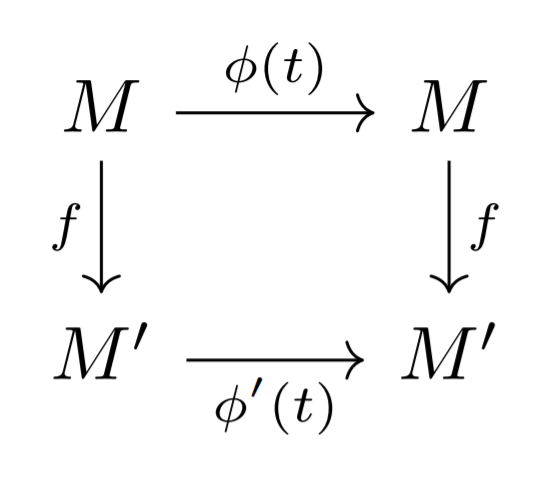
The idea is that topological conjugacies should "send flows to flows". The commutative diagram says that if you advance $ \phi'$ for time $ t$ and then change the manifold you're interested in, this is the same as first changing the manifold you're interested in and then advancing $ \phi'$ forward by time $ t$.

Thinking of $ \phi : \mathbb{R} \to \mathsf{Diff}$ and $ \phi : \mathbb{R} \to \mathsf{Diff}$ as $ \mathsf{Diff}$-functors the above diagram gives that $ f$ is the unique component of a natural transformation between $ \phi$ and $ \phi'$. This motivates the following definition:

Definition: Let $ \mathsf{Dynam}$ be the category

$ \mathsf{Diff}^{\mathbb{R}}$

i.e. the category where

• objects are functors $ \phi : \mathbb{R} \to \mathsf{Diff}$ and
• morphisms are natural transformations $ f : \phi(\cdot) \to \phi'(\cdot)$.

Because $ \mathsf{Dynam}$ is a functor category and $ \mathsf{Diff}$ is nice we get lots of things for free.

Corollary: (yes to a definition) $ \mathsf{Dynam}$ has finite colimits, finite limits, and is cartesian closed.

$ \mathsf{Dynam}$ inherits all the niceness from $ \mathsf{Diff}$ as described in this nLab article. A fun (?) exercise is to see what the limits and colimits in $ \mathsf{Dynam}$ are like by computing some examples.